Tutorial 07: Data wrangling and cross validation (solutions)

Introduction

In this lab session you will explore

Data wrangling; restructuring data frames
Graphical data exploration
Cross validation

Open your github repository clone project from Lab 2 or 4
During this lab, you can work in a .R file, but working with code chunks in a .Rmd is recommended.
Make sure you update the StatCompLab package to version 21.7.0 or higher.

Throughout this tutorial, you’ll make use of the data wrangling and plotting tools in the dplyr, magrittr, ggplot2 and other tidyverse packages, so start your code with library(tidyverse) and library(StatCompLab).

Note that the exercises in this tutorial build on each other, often with one solution being similar to previous solutions, with just a few additions and/or modifications.

Some of the data wrangling functions used in the tutorial are

mutate to add or alter variables
filter to keep only rows fulfilling given criteria
group_by to perform analyses within subgroups defined by one or more variables
summarise to compute data summaries, usually with subgroups
select to keep only some variables
left_join to join two data frames together, based on common identifier variables
pivot_wider to split a value variable into new named variables based on a category variable
pivot_longer to gather several variables into a new single value variable, and the names stored in a new category variable
%>%, the “pipe” operator used to glue a sequence of operations together by feeding the result of an operation into the first argument of the following function call
head to view only the first few rows of a data frame. This can be useful when debugging a sequence of “piped” expressions, by placing it last in the pipe sequence
pull to extract the contents of a single variable

Functions for plotting,

ggplot for initialising plots
geom_point for drawing points
facet_wrap for splitting a plot into “facet” plots, based on one or more category variables

Scottish weather data

The Global Historical Climatology Network at https://www.ncei.noaa.gov/products/land-based-station/global-historical-climatology-network-daily provides historical weather data collected from all over the globe. A subset of the daily resolution data set is available in the StatCompLab package containing data from eight weather stations in Scotland, covering the time period from 1 January 1960 to 31 December 2018. Some of the measurements are missing, either due to instrument problems or data collection issues. Load the data with

data(ghcnd_stations, package = "StatCompLab")
data(ghcnd_values, package = "StatCompLab")

The ghcnd_stations data frame has 5 variables:

ID: The identifier code for each station
Name: The humanly readable station name
Latitude: The latitude of the station location, in degrees
Longitude: The longitude of the station location, in degrees
Elevation: The station elevation, in metres above sea level

The station data set is small enough that you can view the whole thing, e.g. with knitr::kable(ghcnd_stations). You can try to find some of the locations on a map (google maps an other online map systems can usually interpret latitude and longitude searches).

Solution:

knitr::kable(ghcnd_stations)

ID	Name	Latitude	Longitude	Elevation
UKE00105874	BRAEMAR	57.0058	-3.3967	339
UKE00105875	BALMORAL	57.0367	-3.2200	283
UKE00105884	ARDTALNAIG	56.5289	-4.1108	130
UKE00105885	FASKALLY	56.7181	-3.7689	94
UKE00105886	LEUCHARS	56.3767	-2.8617	10
UKE00105887	PENICUIK	55.8239	-3.2258	185
UKE00105888	EDINBURGH: ROYAL BOTANIC GARDE	55.9667	-3.2100	26
UKE00105930	BENMORE: YOUNGER BOTANIC GARDE	56.0281	-4.9858	12

The ghcnd_values data frame has 7 variables:

ID: The station identifier code for each observation
Year: The year the value was measured
Month: The month the value was measured
Day: The day of the month the value was measured
DecYear: “Decimal year”, the measurement date converted to a fractional value, where whole numbers correspond to 1 January, and fractional values correspond to later dates within the year. This is useful for both plotting and modelling.
Element: One of “TMIN” (minimum temperature), “TMAX” (maximum temperature), or “PRCP” (precipitation), indicating what each value in the Value variable represents
Value: Daily measured temperature (in degrees Celsius) or precipitation (in mm)

The values data object has 502901 rows, so we don’t want to try to view the whole object directly. Instead, we can start by summarising it.

Start by counting how many observations each station has, for each type of measurement. The shortest approach is to use the count() function. A more generalisable approach is to use the group_by(), summarise(), and n() functions. See the description on ?count for how count() is connected to the others. To avoid having to create temporary named variables, end the pipe operations with a call to knitr::kable(), especially if you’re working in an RMarkdown document.

Solution:

ghcnd_values %>%
  count(ID, Element) %>%
  knitr::kable()

ID	Element	n
UKE00105874	PRCP	20301
UKE00105874	TMAX	21399
UKE00105874	TMIN	21277
UKE00105875	PRCP	20668
UKE00105875	TMAX	21514
UKE00105875	TMIN	21523
UKE00105884	PRCP	20575
UKE00105884	TMAX	20861
UKE00105884	TMIN	20856
UKE00105885	PRCP	19449
UKE00105885	TMAX	19451
UKE00105885	TMIN	19547
UKE00105886	PRCP	21550
UKE00105886	TMAX	21548
UKE00105886	TMIN	21548
UKE00105887	PRCP	20684
UKE00105887	TMAX	21087
UKE00105887	TMIN	21130
UKE00105888	PRCP	21184
UKE00105888	TMAX	21483
UKE00105888	TMIN	21540
UKE00105930	PRCP	21184
UKE00105930	TMAX	21015
UKE00105930	TMIN	21527

Exploratory plotting

Before, we only looked at the station data and weather measurements separately. When plotting, we would at least like to have access to the station names instead of the identifying codes, to give a more humanly readable presentation.

This can be accomplished with the left_join() function, that can add copies of the rows from one data frame to another, where one or more columns match. Create a new variable, ghcnd that for each observation contains both the measurements and the station data:

ghcnd <- left_join(ghcnd_values, ghcnd_stations, by = "ID")
head(ghcnd)

## # A tibble: 6 × 11
##   ID           Year Month   Day DecYear Element Value Name    Latitude Longitude
##   <chr>       <int> <int> <int>   <dbl> <chr>   <dbl> <chr>      <dbl>     <dbl>
## 1 UKE00105874  1960     1     1   1960  TMAX      3.9 BRAEMAR     57.0     -3.40
## 2 UKE00105874  1960     1     1   1960  TMIN      3.3 BRAEMAR     57.0     -3.40
## 3 UKE00105874  1960     1     2   1960. TMAX      7.2 BRAEMAR     57.0     -3.40
## 4 UKE00105874  1960     1     2   1960. TMIN     -8.3 BRAEMAR     57.0     -3.40
## 5 UKE00105874  1960     1     3   1960. TMAX      6.7 BRAEMAR     57.0     -3.40
## 6 UKE00105874  1960     1     3   1960. TMIN     -6.7 BRAEMAR     57.0     -3.40
## # ℹ 1 more variable: Elevation <dbl>

Now plot daily minimum and maximum temperature measurements connected by lines as a function of time (DecYear), with a different colour for each element, and a separate subplot for each station (facet_wrap(~variablename)), labeled by the station names.

Again, avoid creating a temporary named variable. Instead, feed the initial data wrangling result into ggplot() directly.

Solution:

ghcnd %>%
  filter(Element %in% c("TMIN", "TMAX")) %>%
  ggplot(aes(DecYear, Value, colour = Element)) +
  geom_line() +
  facet_wrap(~ Name)

Due to the amount of data, it’s difficult to see clear patterns here. Produce two figures, one showing the yearly averages of TMIN and TMAX as points, and one showing the monthly seasonal averages (for months 1 through 12) of TMIN and TMAX, separately for each station.

Again, avoid creating a temporary named variable. In the previous code, insert calls to group_by() and summarise(), and modify the x-values in the aesthetics.

What are the common patterns in the yearly values, and in the monthly seasonal values?

Solution:

The yearly averages all seem to have a slight increasing trend:

ghcnd %>%
  filter(Element %in% c("TMIN", "TMAX")) %>%
  group_by(ID, Name, Element, Year) %>%
  summarise(Value = mean(Value), .groups = "drop") %>%
  ggplot(aes(Year, Value, colour = Element)) +
  geom_point() +
  facet_wrap(~ Name)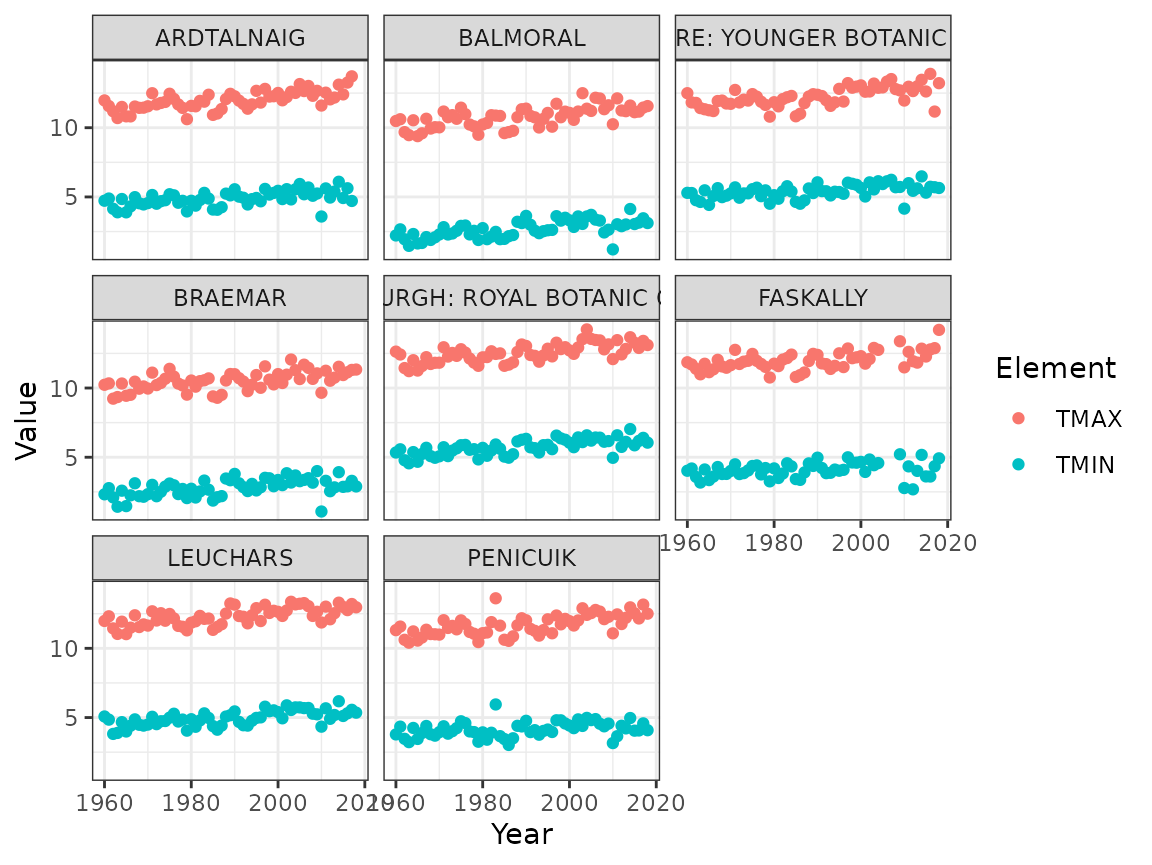

The monthly seasonal averages clearly show the seasonal pattern. The shapes are similar for all stations, but the average and amplitude varies a bit:

ghcnd %>%
  filter(Element %in% c("TMIN", "TMAX")) %>%
  group_by(ID, Name, Element, Month) %>%
  summarise(Value = mean(Value), .groups = "drop") %>%
  ggplot(aes(Month, Value, colour = Element)) +
  geom_point() +
  facet_wrap(~ Name)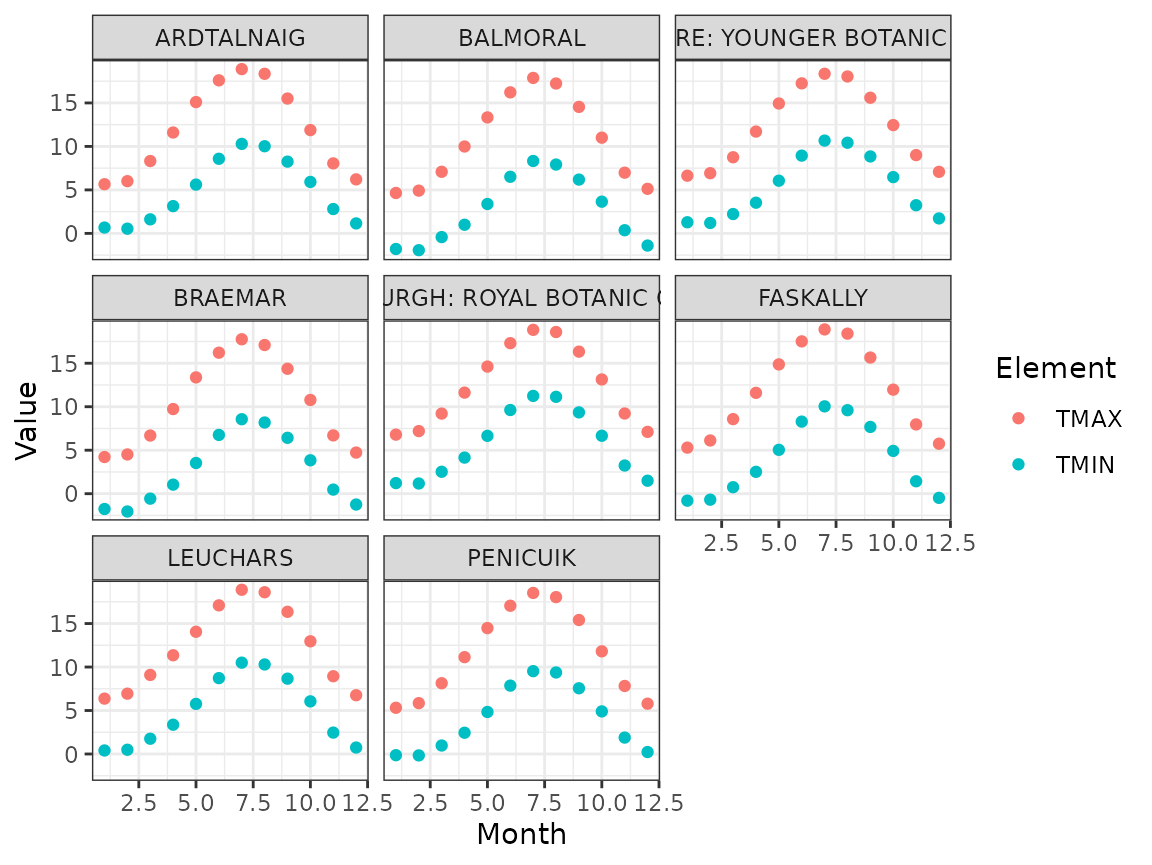

Scatter plots

If we want to do a scatter plot of TMIN and TMAX, we need to rearrange the data a bit. For this we can use the pivot_wider function, that can turn a name variable and a values variable into several named variable. Note that if only some measurement elements are present on a given day, NA’s will be produced by default. Optionally, filter these rows out before calling ggplot().

Draw a scatterplot for daily TMIN vs TMAX for each station, with colour determined by the month.

Solution:

ghcnd %>%
  pivot_wider(names_from = Element, values_from = Value) %>%
  filter(!is.na(TMIN) & !is.na(TMAX)) %>%
  ggplot(aes(TMIN, TMAX, colour = factor(Month))) +
  geom_point() +
  facet_wrap(~ Name)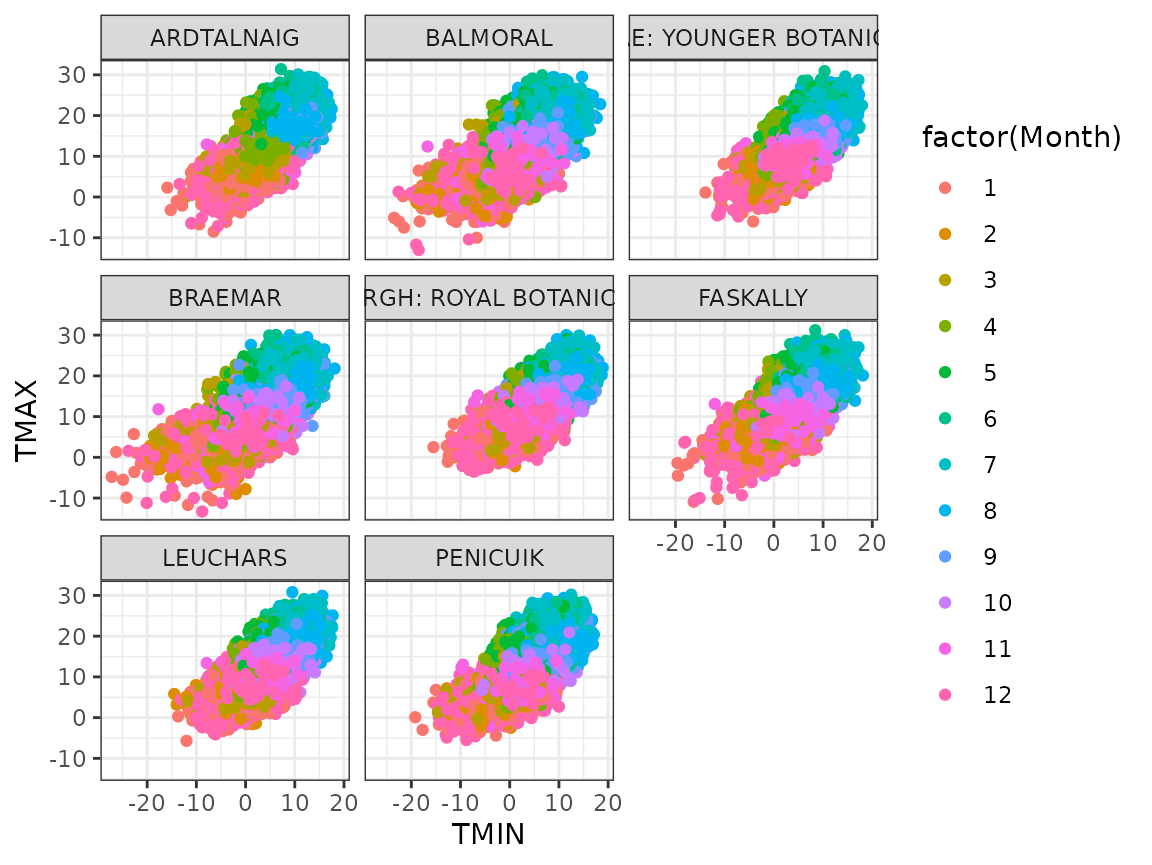

Cross validation

Choose one of the stations, and create a new data variable data from ghcnd with the yearly averages of TMIN as a column (as in the previous pivot_wider output), with missing values removed with filter().

Solution:

data <- ghcnd %>%
  filter(ID == "UKE00105875") %>%
  pivot_wider(names_from = Element, values_from = Value) %>%
  filter(!is.na(TMIN)) %>%
  group_by(ID, Name, Year) %>%
  summarise(TMIN = mean(TMIN), .groups = "drop")

Within-sample assessment

Now, using the whole data estimate a linear model for TMIN, with lm() formula TMIN ~ 1 + Year, and compute the average 80% Interval score (use proper_score() that you used in lab 6) for prediction intervals for each of the TMIN observations in data. See ?predict.lm for documentation for the predict() method for models estimated with lm().

Solution:

fit0 <- lm(TMIN ~ 1 + Year, data = data)
pred0 <- predict(fit0, newdata = data,
                 interval = "prediction", level = 0.8)
score0 <- mean(proper_score(
  "interval", data$TMIN,
  lwr = pred0[, "lwr"], upr = pred0[,"upr"], alpha = 0.8))

Cross validation

We now want to compute the 5 average 80% Interval scores from 5-fold cross validation based on a random partition of the data into 5 approximately equal parts.

First add a new column Group to data defining the partitioning, using mutate(). One approach is to compute a random permutation index vector, and then use the modulus operator %% to reduce it to 5 values, or ceiling() on scaled indices.

Solution:

data <- 
  data %>%
  mutate(Group = sample(seq_len(nrow(data)), size = nrow(data), replace = FALSE),
         Group = (Group %% 5) + 1)
# Alternative:
# data <- 
#  data %>%
#  mutate(Group = sample(seq_len(nrow(data)), size = nrow(data), replace = FALSE),
#         Group = ceiling(Group / nrow(data) * 5))

Then loop over the partition groups, estimating the model leaving the group out, and then predicting and scoring predictions for the group.

Compare the resulting scores with the one based on the whole data set. Is the average cross validation score larger or smaller?

Solution:

scores <- numeric(5)
for (grp in seq_len(5)) {
  fit <- lm(TMIN ~ 1 + Year, data = data %>% filter(Group != grp))
  pred <- predict(fit, newdata = data %>% filter(Group == grp),
                     interval = "prediction", level = 0.8)
  scores[grp] <- mean(proper_score(
    "interval",
    (data %>% filter(Group == grp)) %>% pull("TMIN"),
    lwr = pred[, "lwr"], upr = pred[,"upr"], alpha = 0.8))
}

The average cross validation score for this problem is usually larger than the one for the whole data set; it’s is intended to reduce the risk of underestimating the prediction error, so this is what we would expect. Repeat the random group allocation to see how much it influences the cross validation score average.

knitr::kable(data.frame("Whole data score" = score0,
                        "Cross validation score" = mean(scores)))

Whole.data.score	Cross.validation.score
1.400015	1.424231

Finn Lindgren

Introduction

Scottish weather data

Exploratory plotting

Scatter plots

Cross validation

Within-sample assessment

Cross validation